Entropy is a property of systems which are described in terms of work, heat, and temperature differences. The study of such systems is the subject of Thermodynamics. In order to attempt to understand the concept of entropy, it is best to begin by clarifying concepts associated with energy.
Energy can be designated by the symbol E, and has units of Joules (as well as units of calories, electron-Volts, etc. — a calorie is equal to 4.186 Joules at 15ºC). Energy consists of macroscopic energy and microscopic energy. Notable forms of macroscopic energy are kinetic energy and potential energy. It is possible to measure the kinetic and gravitational potential energy of an object by defining these terms relative to the surface of the Earth. But there is no absolute (non-relative) kinetic or gravitational potential energy of any object having no frame of reference.
The microscopic energy of an object (the energy of an object's molecules and subatomic particles) is called the internal energy (designated by the symbol U). It is not possible to measure or quantify the total internal energy of an object even in relative terms. Only the change in internal energy (ΔU) is meaningful. Internal energy includes such things as the translational kinetic energy of molecules (corresponding to the temperature of an object), the rotational energy of molecules, the vibrational energy of molecules and the energy of chemical bonds of molecules as well as intermolecular forces and subatomic particle energy. Kinetic energy and potential energy can be quantified relative to a point on the Earth, but there is no reference point against which the many forms of internal energy can be quantified. (A glucose molecule at zero Kelvin will have internal energy.)
A change of energy is the difference between the initial and final states of an object or system, represented by the symbol ΔE.
Mathematically: ΔE = Efinal − Einitial
According to the First Law of Thermodynamics, energy is neither created nor destroyed (i.e.,the net energy of the universe never changes), which means that the total ΔE must always be zero. But forms of energy can change, such as Kinetic Energy (KE) and gravitational Potential Energy (PE). If an apple falls from a tree, the gravitational potential energy of the apple decreases while the kinetic energy of the apple increases as the apple falls. When the apple hits the ground, kinetic energy of the apple becomes zero, and the internal energy of the apple and Earth (totalled for both) increases by an amount equal to the decrease in kinetic energy.
Mathematically: ΔE = ΔPE + ΔKE + ΔU = 0 (First Law of Thermodynamics)
As the apple falls there is a decrease in gravitational potenial energy (ΔPE is negative) that exactly equals the increase in kinetic energy (the positive value of ΔKE), which nets to zero. Until the apple hits the ground, ΔU is zero. After the apple hits the ground there is no more kinetic energy (KE = 0) and the decrease in potential energy (negative ΔPE) is exactly equal and opposite to the increase in internal energy (positive ΔU).
For a gas, there is a form of energy represented as the product of pressure (P) and volume (V), which is represented as PV. The PV energy in a balloon will increase as the temperature or number of molecules in the balloon increases: the volume of the balloon will increase, the pressure in the balloon will stay the same, and the product of pressure and volume will increase. If a gas is in a sealed metal container with rigid walls instead of in a balloon, the PV energy in the container will still increase as the temperature or number of molecules in the container increases: the pressure in the container will increase, the volume of the container will stay the same, and the product of pressure and volume will increase. PV energy is independent of internal energy, but is dependent upon Temperature (symbol T) and the number of molecules in the system for which PV energy is being quantified. Unlike other forms of energy, PV energy can be quantified in absolute (non-relative) terms.
Mathematically: PV = nRT where n is the number of molecules (in moles) and R is the universal gas constant. (The equation is only exactly correct for an ideal gas, which represents molecules as infinitesimal particles that exert no attractive or repulsive force.)
The sum of internal energy and PV energy defines a form of energy called the enthalpy (symbol H). Enthalpy is thermal energy, i.e., the energy associated with changes in temperature. Enthalpy includes PV energy, which varies with temperature (nRT) and with the internal energy associated with chemical reactions. Although enthalpy is often equated with heat (the term enthalpy comes from the Greek word enthalpien, which means "heat"), in Thermodynamics enthalpy is distinct from heat (symbol Q) and is distinct from internal energy (U).
Mathematically, enthalpy is defined as: H = U + PV
Because enthalpy includes internal energy, total enthalpy of a system or object cannot be quantified or measured directly. But enthalpy change (ΔH) can be measured. For an exothermic (energy-releasing) chemical reaction ΔH is the energy generated by the reaction (including the PV term for ambient pressure resistance). ΔH is negative for an exothermic chemical reaction (the enthalpy of the system or object is reduced) whereas ΔH is positive for an endothermic (energy-absorbing) chemical reaction (the enthalpy of the system or object is increased by the amount of energy absorbed).
Although work (symbol W) can be quantified in energy units (Joules), work is not a form of energy. Work is a means of transferring energy. Objects or systems have properties such as temperature, pressure, mass, volume, energy, etc., but work is not a property. An object can be said to contain energy, but an object cannot be said to contain work. If work is done on an object to increase the object's velocity, the kinetic energy of the object will increase, but the object is not said to contain more (or any) work. Work is simply a process by which the energy of an object can be changed. Work is the product of Force (F) and the length (L) of the distance over which that force is applied: W = F x L. A ball being thrown will accelerate in the hand of the thrower over the distance through which the hand forcefully moves. The work accomplished by the force of the thrower's hand increases the kinetic energy of the ball. Gravitational force exerted downward on a book sitting on a table is opposed by an equal upward force from the table, the book does not move, and no work is done by either force. In thermodynamics, work is often the work of compression or expansion by a piston on a gas contained in a fixed volume chamber ("PV work").
Heat (symbol Q), like work, can be quantified in Joules, calories or other units of energy. Like work, in Thermodynamics it is incorrect to describe heat as a form of energy. An object does not contain a defined amount of heat, just as an object does not contain a defined amount of work. Like work, heat is a means of energy transfer (generally because of a temperature difference). Energy is transferred, heat is not transferred. Heat is simply a process by which the thermal energy of an object can be changed. The transfer of one calorie of thermal energy to one gram of water will raise the temperature of the water from 14.5ºC to 15.5ºC (by definition of calorie). The idea that heat is an entity that flows like a fluid was part of the discredited idea that heat is "phlogiston". Despite the fact that phlogiston theory has long been discredited, the terminology with heat is often abused and with such phrases as "heat content", "flow of heat" and "heat transfer". It is so awkward to avoid these phrases that no attempt is generally made to do so, despite the literal inaccuracy. "Heat" is being used to represent "thermal energy" in these cases, rather than the process of thermal energy transfer.
If a wooden block is pushed along a table-top, the force pushing the block is opposite to the frictional force in the table-top, which results in some of the work being transformed into heat.
The change in enthalpy due to a process is not the same as the change in heat due to a process, because enthalpy is a form of energy, but heat is a means of energy transfer. A given change in the internal energy portion of enthalpy (thermal energy) may involve a mixture of heat and work energy transfers. Only by studying the process can the relative contribution of work and heat to final internal energy be determined.
Mathematically: dU = δQ + δW
In words: the change in internal energy is the sum of the energy change due to heat plus the energy change due to work. Although internal energy is the sum of work and heat, the more usual covention is to write the formula as: dU = δQ − δW because of the original application of thermodynamics to heat engines, which output work from an input of heat. The internal energy change is the difference between the heat added and the work removed from the system. dU differs from ΔU in that ΔU represents a finite change whereas dU represents an infinitesimal change. The infinitesimal change of internal energy is a sum of infinitesimal changes of energy due to heat and work. The symbols δQ & δW are used rather than the symbols dQ & dW to denote the fact that the exact contributions of either the heat or the work term cannot be determined. Only the sum of energy change due to both heat and work can be determined exactly.
The First Law of Thermodynamics states that energy is conserved, i.e., energy is neither created nor destroyed (E = mc2 is beyond the scope of Thermodynamics, but total of mass and energy would be conserved). The expression ΔE = ΔPE + ΔKE + ΔU + PΔV = 0 is thus a statement of the First Law of Thermodynamics in expressing the fact that although potential, kinetic, internal, and PV energy may change as a result of a process, total energy does not change.
The equation dU = δQ + δW is also sometimes used as a statement of the First Law of Thermodynamics, despite the fact that it is restricted to internal energy rather than all forms of energy. Neither work nor heat are forms of energy or are properties of objects or systems. But they are processes that can change the internal energy of an object or system. An somewhat poor analogy would be to have a bank balance representing internal energy, an to have work and heat represent cash and checks. A bank balance can be altered by deposits or withdrawals of checks or cash, but neither checks nor cash are a bank balance.
Entropy (designated by the symbol S) is an elusive concept that is defined in terms of other elusive concepts. Entropy quantifies energy not available to do work, but entropy can either increase or decrease in a reversible process, and entropy is not quantified in units of energy. The units of entropy are Joules per Kelvin (J/K). Joules are a unit of energy, work or heat, but in the context of the units of entropy, Joules quantifies only heat. So the units of entropy can be described as heat divided by temperature. Like mass, energy or volume, entropy is a property of an object or system.
Entropy is always associated with the heat form of energy transfer. In general, the entropy of an object or system can increase or decrease, associated with thermal energy being transferred into or out of an object or system ("flow of heat" in or out). Although the entropy of an object or system can increase or decrease, the entropy of the universe as a whole can never decrease. As stated in the Second Law of Thermodynamics, for any process, the entropy of the universe will either stay the same or increase, but never decrease. Only for a reversible process can the entropy of the universe remain unchanged. For every irreversible process (i.e., every real process) the entropy of the universe increases. The direction of heat transfer is the same as the direction of entropy transfer. When heat is transferred out of a system, entropy is transferred out of the system. When heat is transferred into a system, entropy is transferred into the system.
The following are equivalent statements of the Second Law of Thermodynamics.
The Second Law according to Lord Kelvin (William Thompson):
There can be no engine, which when operating in cycles, the sole effect of which is pumping energy from one heat-reservoir and completely converting it into work.
Essentially: heat cannot be converted entirely into work.
The Second Law according to Rudolf Clausius (first formulation):
There can be no process the sole result of which is a flow of energy from a colder to a hotter body.
The Second Law according to Rudolf Clausius (second formulation):
In any spontaneous process, occurring in an isolated system, the entropy never decreases.
Mysteriously, the property entropy is calculated by dividing the non-property heat by the property temperature.
Mathematically: dS = (δQR)/T or S = ∫(δQR)/T
QR is thermal energy transfer that is Reversible.
The conversion of one mole of ice into water is a reversible process that occurs at constant temperature (about 273 Kelvins) with about 6000 Joules of heat. Thus,
ΔS = 6000/283 = 22 Joules/Kelvins.
Mathematically, the product of Temperature and Entropy is an energy term (a consequence of the fact that entropy is equal to heat, quantified as energy, divided by temperature). For this reason, Temperature multiplied by an infinitesimal amount of Entropy (TdS) can be equated to infinitesimals of internal energy, enthalpy, volume and pressure:
TdS = dU + pdV
TdS = dH − Vdp
TdS = CPdT − RT(dP/P)
where CP is the heat capacity at constant pressure and R is the gas constant. "Heat capacity" is the amount of heat required to raise temperature a given amount. One calorie of heat will raise the temperature of one gram on water by 1ºC at 15ºC. CP is "entropy per degree".
The entropy change of any process will be the sum of the entropy transfer (into or out of a system) plus the entropy production of the process. The amount of entropy produced by a process is a measure of the irreversibility of the process. An irreversible process accomplishes the maximal amount of work from a given amount of heat. But in every real process that extracts work from heat, heat is lost, resulting in an increase in the entropy of the universe (associated with heat that can no longer do work).
Mathematically: dS = (δQR)/T + σ
In words: the change in entropy is the sum of (reversible) entropy transfer [(δQR)/T] plus entropy production [σ].
Another way to attempt to understand entropy is to look at how the concept is used. The Second Law of Thermodynamics states that for any process, entropy in the universe either increases or does not change, but never decreases (although the entropy of an isolated system can decrease by contact with another system). Only if a process is reversible does the entropy of the universe not change.
What are examples of irreversible processes?
Entropy provides a means of quantifying irreversibility. In an irreversible process the amount of entropy of the universe increases. The amount of entropy increase in the universe associated with an irreversible process corresponds to the amount of energy that is no longer available to perform work.
The entropy of an isolated system increases as the state of equilibrium is approached. Equilibrium corresponds to maximum entropy (maximum disorder). Systems spontaneously proceed toward an equilibrium state (maximum entropy).
The Kelvin-Plank version of the Second Law of Thermodynamics states that it is impossible for an engine working in a cycle to covert heat entirely into work. For example, heat (QH) could flow into a chamber and cause pressure in the chamber to increase enough to move a piston. But in a real process, the energy corresponding to the amount of work (W) performed in moving the piston will always be less than the energy corresponding to the amount of heat (QH) that caused the gas to expand. Some heat (QC) will have been lost. The amount of entropy increase in the universe (ΔSu) corresponds to QC divided by the temperature (TC) of the lowest temperature heat sink to which the lost heat flowed. (This model of quantifying irreversibility is not so easily applied to the processes described in the previous section.)
The most efficient processes will be those that occur with a minimal increase in entropy. Thus, imaginary reversible processes (cycles) that involve no entropy production provide a quantifiable theoretical standard for optimal performance that can be compared to real processes (real cycles, real engines).
What is an example of a reversible process? There are no reversible processes in the real world, but physicists can fantasize a reversible process in the same way as they can fantasize a block sliding on a frictionless surface forever with an unchanging velocity.
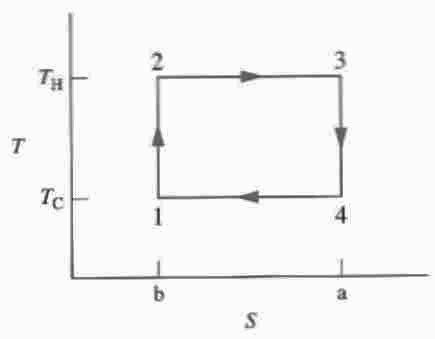
A Carnot Cycle is an imaginary reversible process. A Carnot Cycle consists of two adiabatic work processes and two isothermal heat transfer processes.
An adiabatic work process is a work process that occurs without any heat transfer. There can be no entropy change in an adiabatic process because entropy change is always associated with a heat transfer. Therefore, adiabatic work processes are reversible and involve no entropy change. In a graph of Pressure versus Volume (PV graph), pressure drops most steeply as an adiabatic expansion begins, and drops increasingly less steeply as the expansion proceeds. Between two points on a PV graph, there can be many different possible adiabatic expansion curves, but all those curves will have the same entropy on each point of the curve.
An isothermal heat transfer process is a heat transfer process that occurs without any temperature change. In the Carnot Cycle, one isothermal heat transfer occurs with a hot reservoir and the other isothermal heat transfer occurs with a cold reservoir. The entropy increase (ΔSH) that occurs with the isothermal heat transfer (QH) at the hot reservoir (TH) is exactly equal to the entropy decrease (ΔSC) that occurs with the isothermal heat transfer (QC) at the cold reservoir (TC). Thus, the entropy increase from the hot reservoir and the entropy decrease to the cold reservoir results in no net entropy change for the Carnot Cycle.

|
Mathematically: ΔSH = +|QH|/TH (hot reservoir)
and ΔSC = −|QC|/TC (cold reservoir)
Note that negative change in entropy means that entropy is decreasing. Entropy is never negative.
In sum, the adiabatic work processes are reversible and involve no entropy change. The isothermal entropy increase and decrease associated with the two heat transfers are equal and opposite — canceling each other out to give no net entropy change. So the final entropy change after completion of one Carnot Cycle is zero, and the Carnot Cycle is reversible. Four processes in the Cycle occur which cause a change of state between four states (1,2,3,4), which can be represented as points on a PV (Pressure-Volume) graph. The four processes in the Cycle can be graphed as curves which depict the pressure and specific volume changes as each process proceeds between states. The Cycle can also be graphed in a similar manner on a TS (Temperature-Entropy) graph, which results in vertical or horizontal straight lines for each process connecting two states.
A Carnot Engine is an imaginary reversible engine that is based
on the Carnot Cycle. Gas expands and is compressed in a chamber adjoining
a frictionless piston. An equal amount of work is done by and on the piston.
An equal amount of heat is transferred in as is transferred out of the
chamber.
| Process 1 → 2 | Process 2 → 3 | Process 3 → 4 | Process 4 → 1 | Carnot Power Cycle |
|---|---|---|---|---|
![[ Process 1 → 2 ]](P12.jpg)
|
![[ Process 2 → 3 ]](P23.jpg)
|
![[ Process 3 → 4 ]](P34.jpg)
|
![[ Process 4 → 1 ]](P41.jpg)
|
![[ Carnot Power Cycle ]](CarnotC.jpg)
|
The final process returns the Carnot Engine to the original position of the piston and the original temperature, completing the cycle.
Process 2 → 3 and process 4 → 1 might seem especially mysterious insofar as these steps involve a heat flow without a temperature difference. How can heat flow if there is no temperature difference to drive the process? What is the motive force? Actually, heat can flow from one body to another at the same temperature if one of the bodies is undergoing a phase change (gas to liquid or liquid to solid) because heat is absorbed or released during a phase change, even though temperature does not change. Conceivably, the chamber at temperature TH could be in contact with a vast thermal reservoir undergoing a gas to liquid phase transition (releasing heat into the chamber at TH). The material in the hot reservoir would have a much higher vaporization temperature than the gas in the chamber that is absorbing heat. The chamber at temperature TC could be in contact with a vast thermal reservoir undergoing a solid to liquid phase transition (absorbing heat from the chamber at TC).
In process 4 → 1, for
example, an infinitesimal amount of compression would tend
to cause an infinitesimal rise in temperature. But because
the compression chamber is not insulated, but is imagined
to be in thermal contact with a huge (infinite) reservoir
at TC, the infinitesimal temperature rise
in the compression chamber causes an infinitesimal flow
of heat (energy) out of the compression chamber,
thereby keeping the temperature in the compression
chamber at TC. An infinite number of such
infinitesimal steps result in a finite isothermal
compression in which temperature remains at TC.
A problem with this is that an infinitesimal heat
flow at an infinitesimal temperature difference should
correspond to an infinitesimal irreversibility. If
an infinite number of infinitesimal compressions can
sum to a finite compression, then an infinite
number of infinitesimal irreversibilities should
sum to a finite irreversibility. But through the
magic of thought experiment it is claimed that
infinitesimal compressions produce equilibrium
states rather than infinitesimal non-equilibrium
states, that these infinitesimal equilibrium
states are reversible, and sum to a finite
reversible state.
The entropy change when one mole of water boils to form one mole of gaseous water at a constant temperature of T = 100ºC = 373 Kelvins can be calculated from the enthalpy of vaporization (ΔHvap = 40.67 KiloJoules/mole):
ΔSvap = ΔHvap/T
= [mole X (40.67 kJ/mole)(1000 Joules/kJ)]/373 Kelvins
= 109 J/K
For the reversible isothermal expansion of one mole of an ideal gas from V1 = 1.0 liter to V2 = 2.0 liters the increase in entropy will be:
ΔS = Qrev/T = nR ln (V2/V1)
= mole X [8.3 Joules/(mole X Kelvins)] X ln (2.00)
= 8.3 X 0.67 Joules/Kelvins) = 5.7 J/K
|
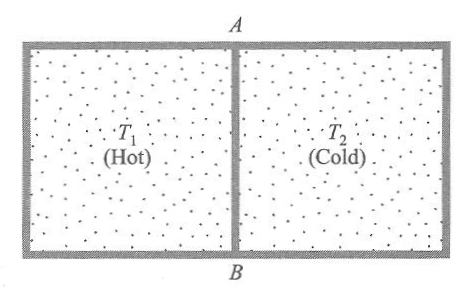
Two containers at different temperatures each containing 1.000 kilograms of water are brought into thermal contact. One container is just below boiling temperature (T1 = 100ºC = 373 Kelvins) and the other container is just above freezing (T2 = 0ºC = 273 Kelvins). Find the net change of entropy when the two containers reach 50ºC = 323 Kelvins. The specific heat of water at constant pressure is CP=4184 J/K
ΔS = ΔS1 + ΔS2
= ∫T1initialT1final CP (dT1)/T1 + ∫T2initialT2final CP (dT2)/T2
= CP [ ln (T1initial/T1final) + ln (T2initial/T2final) ]
= 4184 J/K [ ln (323K/273K) + ln (323K/373K) ] = 100 J/K
The Third Law of Thermodynamics states that the entropy of perfect crystals of all pure elements and compounds is zero at at temperature of zero Kelvin. The Third Law of Thermodynamics provides a standard for the specification of absolute entropy rather than just entropy change. Absolute entropy is written Sº The absolute entropy of one mole of some common stubstances at 25ºC is given in the following table:
SUBSTANCE | Sº (Joules/Kelvins) | STATE (solid/liquid/gas) |
|---|---|---|
| Diamond (carbon) | 2.4 | solid |
| Graphite (carbon) | 5.74 | solid |
| Copper (Cu) | 33.15 | solid |
| Zinc (Zn) | 41.6 | solid |
| Silver (Ag) | 42.55 | solid |
| Water (H2O) | 69.94 | liquid |
| Mercury (Hg) | 76.02 | liquid |
| Helium (He) | 126.1 | gas |
| Argon (Ar) | 154.7 | gas |
| Nitrogen (N2) | 191.5 | gas |
| Oxygen (O2) | 205.03 | gas |
| Carbon dioxide (CO2) | 213.6 | gas |
For solids, Sº generally increases with atomic number. Larger, more complex molecules have larger Sº.
Air is compressed from a pressure of 100 kiloPascals (P1) to 600 kiloPascals (P2) causing a temperature increase from 17ºC (290 Kelvins) (T1) to 57ºC (330 Kelvins) (T2). Treating air as an ideal gas and using a heat capacity at constant pressure for air of CP = 1.006 kiloJoules/(kilogram . Kelvins) and the (kilogram) gas constant R = 0.287 kiloJoules/(kilogram . Kelvins) gives:
ΔS = CP ln (T2/T1) − R ln (P2/P1)
= (1.006 kJ/kg.K) ln (330K/290K) − (0.287 kJ/kg.K) ln (600 kPa)/(600 kPa)
= −0.3842 kJ/kg.K
An alternate calculation, using table values of Sº for air of T1 = 290 Kelvins and T2 = 330 Kelvins gives:
ΔS = (Sº2 −Sº1) − R ln (P2/P1)
= (1.79783−1.66802) kJ/kg.K) − (0.287 kJ/kg.K) ln (600 kPa)/(600 kPa)
= −0.3844 kJ/kg.K
For large temperature differences the second equation will be more accurate.
The change in Gibbs Free Energy (ΔG) can be used to predict whether a chemical reaction will occur or not. Gibbs Free Energy is a property of a system that is determined by enthalpy and entropy:
ΔG = ΔH − TΔS
Enthalpy change (ΔH) is negative for an exothermic reaction, and if entropy change (ΔS) is positive, both ΔH and − TΔS will cause ΔG to be negative. When ΔG for a reaction is negative at constant temperature and pressure, the reaction will occur spontaneously. When ΔG = 0 at constant temperature and pressure, the system is in equilibrium, and no reaction will occur.
The standare Gibbs Free Energy (Gº) can be calculated from the standard enthalpy of formation (Hfº) and standard entropy (Sº), the values of which can be obtained from tables. As an example, calculate ΔGº for the decomposition of calcium carbonate (CaCO3). At 25ºC, for the reaction:
CaCO3 (solid) ↔ CaO (solid) + CO2 (gas)
ΔHº = Hfº(CaO) + Hfº(CO2fº(CaCO3)
= −635.5 − 393.51 − (−1206.9) = 177.9 KiloJoules
ΔSº = Sº(CaO) + Sº(CO23)
= 39.7 + 213.6 − 92.9 = 160.4 Joules/Kelvins
Thus: ΔGº = ΔHº − TΔSº
= 177.9 − (298.15)(160.4 X 10−3) KiloJoules
= 177.9 − 47.82 KiloJoules
= 130.1 KiloJoules
Because ΔGº is positive, calcium carbonate does not decompose at 25ºC, which means that marble and clam shells (which are composed of CaCO3) are stable at 25ºC.
Thermodynamics preceeded the knowledge that matter is
made of atoms and molecules. With that knowledge, the
absoluteness of the Second Law of Thermodynamics is
replaced with an extremely high probability that (for
example) a gas will expand irreversibly into an
empty chamber.
|
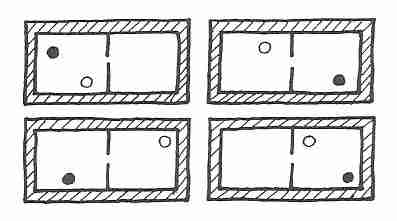
If two different gas atoms are in a box having two
compartments, and there is an opening in the partition
separating the two compartments that will allow the atoms
to pass through, at any one time there will be only one
chance in four that both atoms will be in the left
compartment (Probability = ¼).
|
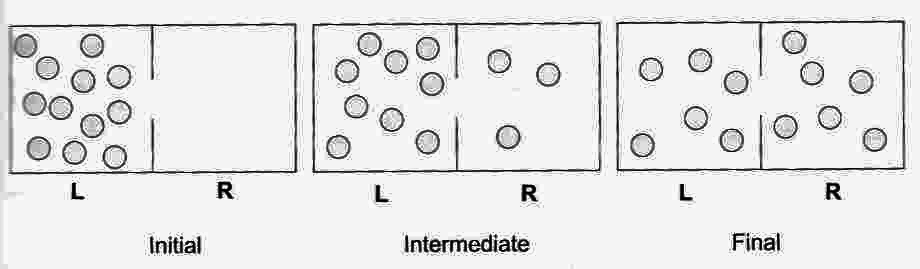
By the same logic, if 12 gas atoms are allowed to equilibrate between two compartments of a box, on average there will be about six atoms in each compartment at the same time — and at any one time there will be only one chance in 24 that all of the gas atoms will be in the left compartment (Probability = 1/24).
Carrying the same logic even further, if billions of atoms
are allowed to equilibrate between two compartments, on average
about half the atoms will be in each compartment, and the
probability is virtually zero that at an one time all of the
atoms will be in the left compartment. The distribution of
atoms into their most probable arrangement corresponds to
an increase in entropy.
|
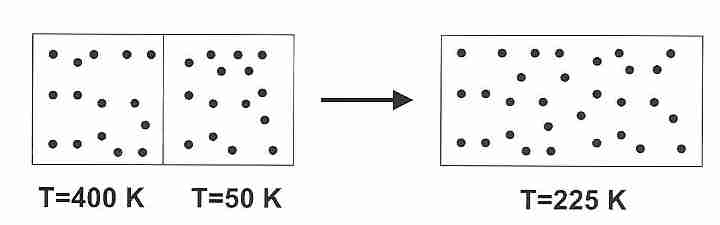
Similarly, if two compartments each contain a gas at different
temperatures (Thot = 400 Kelvins and
Tcold = 50 Kelvins) and the insulating
partition separating the compartments is removed, the gas atoms
will mix to result in an average temperature
(Taverage = 225 Kelvins) and
a net increase in entropy.
Maxwell's Demon was an elf imagined by
James Clerk Maxwell that could violate the Second Law of
Thermodynamics by only allowing fast atoms to pass through
a partition when going to the left side, and only allow
slow atoms to pass through a partition when going to
the right side. Putting energy into a system can
decrease the entropy of the system, but only by
increasing the entropy of the universe. (Presumably
Maxwell's Demon would be burning calories during
his labor.)
|
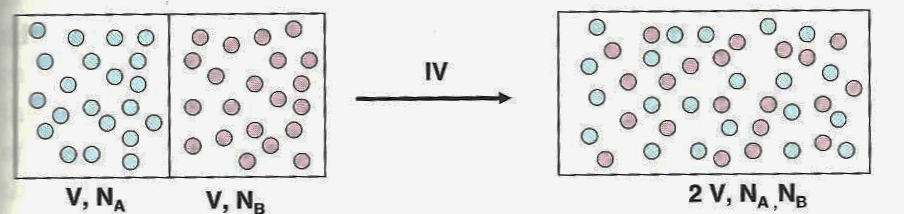
Nonetheless, if a partition separates two different gases
(Helium blue and Argon red, for example) at the same temperature
and pressure, when the partition is removed the two kinds of
atoms will mix, but the entropy does not increase. For
this reason (among others), the equating of entropy with
"disorder" or "mixing" is mistaken.
|
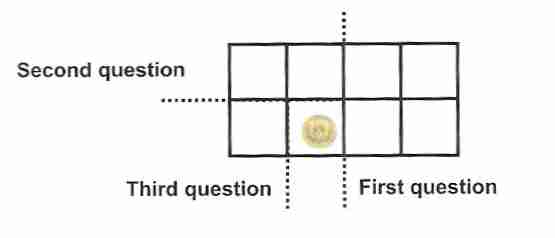
If a coin is hidden in one of eight boxes, there is a 1/8 chance
of guessing which box the coin is in on the first guess. After
guessing four boxes there will be a 50% chance that the
coin has been located. But if the strategy of binary search
is used, the coin can be definitely located in only three
guesses. In the above illustration, the first guess will be
"Is the coin in the left half of the group
of boxes"? The second guess will be "Is the coin in
the lower half of the remaining boxes"? The third and
final guess, which locates the coin, will be "Is the coin in
the left half of the remaining boxes"? The coin was located
in log28 = 3 guesses.
|
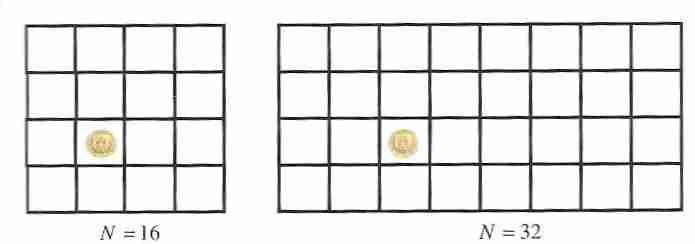
By the same logic, a coin hidden in one of 16 boxes can be located with a binary search in log216 = 4 guesses and a coin hidden in one of 32 boxes can be located in log232 = 5 guesses.
The Austrian physicist Ludwig Boltzmann defined entropy with can the equation:
S = kB log Ω
where kB is the Boltzmann constant and Ω quantifies the total number of microscopic states occupied. The larger the number of occupied microscopic states (i.e., the larger the number Ω). The number Ω is a unitless natural number (0,1,2,3,...). In terms of gas molecules, the number Ω corresponds to all the positions and momenta ("momentums") of all of the gas molecules. Geometrically, the possible microscopic states can be represented as quantized space and momentum, where each quantized position is represented as a tiny cube of three spatial dimensions and each quantized momentum is represented as a tiny "momentum cube" in three momentum dimensions. Combining spatial and momentum dimensions gives a six-dimensional "phase space" containing a finite number of six-dimensional cubes. The very least probable arrangement corresponds to all of the gas molecules being in a single six-dimensional cube of phase space, i.e., Ω = 1 and S = 0. The most probable arrangment will maximize both Ω and S — which will be the equilibrium condition.
kB represents the universal gas constant R per molecule of gas. Thus, the units of kB (J/K) times the natural logarithm of Ω (a unitless natural number) gives the units of S, namely, J/K. By the logic of information theory alluded to above, the base of the logarithm would be 2, i.e., log2. In practice, Ω cannot be determined, the constant kB is a "fudge factor" to make the units come out correctly. The equation S = kB log Ω cannot be proven and cannot be used to calculate either absolute entropy or changes in entropy — it is a conceptual equation rather than an equation that can be used to do actual calculations. Part of the problem with 19th century physicists formulating thermodynamics without understanding that matter is made of atoms, is that they did not realize that temperature is kinetic energy of atoms. If temperature had been defined in units of energy, the "fudge factor" kB would not be needed.
Irreversibility of a process in a limited system need not mean absolute irreversibility of that process in the context of the universe (or wider system). If a hot branding iron is removed from a fire and placed on a rock at normal atmospheric temperature, the branding iron will cool as heat dissipates into the environment from the branding iron. For the limited system of the branding iron, the rock and the air in the vicinity of the branding iron, an irreversible process has occurred. But the cooling of the branding iron is not irreversible in the sense that the branding iron can easily be put back in the fire. If the branding iron is heated to the same temperature it had when it was first removed from the fire, the entropy the branding iron lost during the cooling will be restored to the level of the entropy the iron had when it was first removed from the fire. An irreversible process is still occurring with the fire, but that is outside of the system that is defined to only include the branding iron, the rock and the air in the vicinity of the branding iron. Entropy of the smaller system decreases only as a result of entropy of the larger system increasing.
Similarly, an apple falling from an apple tree represents and irreversible process within the limited system of the apple and the tree. But if a person is added to the system, the person can lift the apple from the ground and place it on a branch of the apple tree. Fat and glucose in the muscle of the person is consumed in an irreversible process that nonetheless provides energy to reverse the process of the apple falling from the tree. Again, entropy of the smaller system decreases only as a result of entropy of the larger system increasing.
A vessel of water placed in a very cold environment will freeze. In forming ice, water molecules organize themselves into a crystal lattice. Although the disorder of the water molecules has decreased, the entropy of the universe as a whole has increased because of the dissipation of heat from the vessel to the cold environment.