With use of suitable cryoprotectants ("anti-freeze" compounds) in cryonics patients, ice crystal damage can be virtually eliminated. (Estimates for recent vitrified cryonics neuro-patients are in the range of 0.2% of water becoming ice.) When biological tissues are vitrified, rather than frozen, they harden slowly like glass, with hardening only being completed in the range of −130ºC. At such low temperatures viscosity is high and damage due to molecular mobility is low. Radiation damage is also minimized, because most of the damaging effects of ionizing radiation are due to the mobility of free-radical atoms or molecules [ULTRAMICROSCOPY; Knopek,E; 10(1-2):71-86 (1982)]. But can mobility & damage be quantified in such a way that the effects over decades or centuries can be estimated?
Molecular mobility for biological samples can be indirectly assayed at dry ice temperature (about −80ºC) on the basis of viability loss over time. Human platelets can be stored at dry ice temperature for up to two years without loss of quality [VOX SANGUINIS; Melaragno,AJ; 49(4):245-258 (1985)]. Red blood cells stored at dry ice temperature as long as 18 years in glycerol have shown breakage rates of 6.7% if transported, and 2.4% if not transported [TRANSFUSION; Valeri,CR; 45(5):822-823 (2005)]. Mouse sperm stored at dry ice temperature for 4 months in a raffinose cryopreservation solution showed only slightly less fertility (71%) than mouse sperm stored at liquid nitrogen temperature for 8 months (73%), but mouse sperm stored for 8 months at dry ice temperature showed significantly less fertility (51%) [EXPERIMENTAL ANIMALS; Okamoto,M; 50(1):83-86 (2001)]. Biochemical studies of 3-to-4 millimeter thick rat liver slices showed only slight decline in enzyme activity after two weeks of storage at dry ice temperature [HISTOCHEMISTRY AND CELL BIOLOGY; Prento,P; 108(6):543-547 (1997)].
Cryobiologist Peter Mazur has stated that below −130ºC "...viscosity is so high (>1013 Poise) that diffusion is insignificant over less than geological time spans." He adds that "...there is no confirmed case of cell death ascribed to storage at −196ºC for some 2-15 years and none even when cells are exposed to levels of ionizing radiation some 100 times background for up to 5 yr." [AMERICAN JOURNAL OF PHYSIOLOGY; Mazur,P; 247(3 Pt 1):C125-C142 (1984)]. Frozen 8-cell mouse embryos subjected to the equivalent of 2,000 years of background gamma rays during 5 to 8 months in liquid nitrogen showed no detrimental effect on survival or development [JOURNAL OF REPRODUCTION AND FERTILITY; Glenister,PH; 70(1):229-234 (1984)].
These assertions are reassuring, but it would be of interest to know what the exact molecular mobilities are in a vitrified solid — or a semi-vitrified human cryonics patient. What may be "insignificant" diffusion for Mazur's purposes may have significant impact in cryonics cases. Information loss is possible in a cell that nonetheless survives. Having some idea of how far, relative to other molecules, a water molecule could move at these temperatures might give some idea of how much "mixing" and "dissolution" is possible over a period of 100 years.
For an ideal gas, a temperature can be expressed as molecular velocity, but for a liquid or solid the bonding between molecules or atoms will significantly affect molecular mobility at low temperatures. It would seem that viscosity would be in direct proportion to molecular mobility, but there is no simple formula to express the velocity of molecules in a solid with a viscosity of 1013 Poise.
The hydrogen bonding in ice is not the same as is seen in water. [See HYDROGEN BONDING by S.Vinogradov&R.Linnel (1971) Section 1-1, and Felix Franks Chapters 3&4]. H-bond enthalpies in ice I vary from 4.7 to 8.2 kcal/mole, whereas H-bond enthalpies in water vary from 1.3 to 2.8 kcal/mole. A water H-bond has an average life of about 2x10−13 second. At 0ºCelcius water molecules experience 1011 to 1012 reorientational and translational movements per second, whereas ice molecules at the same temperature experience 105 to 106 reorientational and translational movements per second. Yet the tetrahedral hydrogen bonds in an ice-crystal lattice are nearly as strong as covalent bonds — in contrast to the random network of bendable, interchangable hydrogen bonds found in liquid water. An ethanol solution is even more highly hydrogen-bonded than water — 98% — but it is still fluid. Molecules in the semi-vitrified solid of a cryonics patient (ice,glycerol/water,salts,protein,fat) would be expected to have more mobility than molecules in an ice crystal — in particular the water molecules which are of concern because of their possible role in dissolution and hydrolysis. Molecules in a fully (<0.2% ice) vitrified cryonics patient (non-glycerol cryoprotectant) would have somewhat more mobility.
At 135 Kelvin (−138º Celcius) vitrified water has a vibrational energy of 17.91 KJoule/mole and a bending energy of 1.93 KJoule/mole as opposed to ice I which has 18.55 and 0 KJoule/mole, respectively. It seems reasonable that the translational motion difference between a crystal and vitreous solid at liquid nitrogen temperature is probably less than an order of magnitude.
It would be nice to have analytical tools with which to quantify possible damage — and a knowledge of molecular mobility at 143 K, 77 K and 4.2 K would be a step in the right direction. Diffusion laws for liquids would seem to be good models for vitrified systems insofar as a vitreous substance at low temperature can be regarded as a highly viscous liquid. Fick's First Law for diffusion would not be appropriate, however:
dc
J = − DA ----
dx
J = rate of diffusion (moles/time)
D = Diffusion coefficient = Mass diffusivity
A = Area across which diffusion occurs
dc/dx = concentration gradient (concentration difference divided by distance)
Fick's First Law states that the rate of diffusion down a concentration gradient is proportional to the instantaneous magnitude of the concentration gradient (which changes as diffusion proceeds). For movement of molecules from a region of higher concentration to a region of lower concentration dc/dx will be negative, so multiplying by −DA gives a positive value to J. Diffusion in a vitrified cryonics patient would presumably not be due to concentration gradients because there should be no concentration gradients. Moreover, Fick's First Law depends on knowing a diffusion coefficient, which is close to what we are trying to determine. Diffusion coefficient is higher for higher temperature and for smaller molecules.
The Einstein-Stokes Equation is a formula for calculation of Brownian Diffusivity, where diffusivity varies directly with absolute temperature and varies inversely with both viscosity and molecular radius:
kT
D = -----
6πrµ
D = Brownian Diffusivity
k = Boltzmann's constant
T = absolute temperature (Kelvins)
r = radius of the molecule
π = 3.14159265358979323... (pi)
µ = viscosity of the medium
Radius is particularly telling because the formula is intended for applicability to large spherical molecules. Of course in a vitrified cryonics patient there is a highly heterogenous mixture of molecules, many of which are quite large or which form membrane barriers (oil-water barriers or large molecule blockade).
A high precision estimate of molecular mobility in a cryonics patient would ultimately have to be determined empirically. Analytically, however, for a given temperature the lower limit of molecular mobility could be that of an ice crystal (perhaps not helpful since this mobility would be close to zero) and the upper limit could be that dictated by the Einstein-Stokes equation using the viscosity and average diameter of a cryoprotectant molecule.
Once a diffusion rate is estimated or determined empirically, the only "small problems" remaining are to determine how long a cryonics patient is expected to be stored before reanimation and to quantify how damaging the determined molecular mobility would be at that temperature.
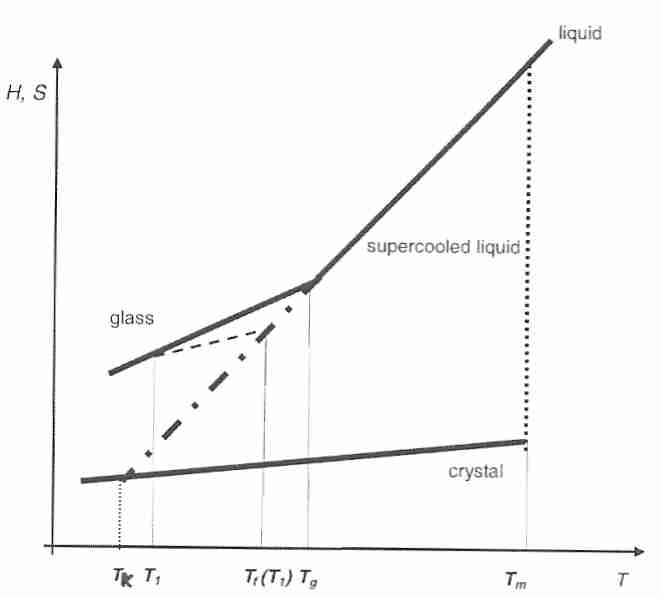
With vitrification a liquid becomes a glass, with a dramatic slowing of diffusive motion of molecules and an apparent loss of ability to flow. But the liquid molecular structure is retained. Translational and rotational motion by molecules nominally ceases at glass transition temperature (Tg), leaving only vibrational motion for thermal energy. A "shoving model", however, holds that some flow does occur within glasses by means of infrequent thermal fluctuations that achieve an activation energy sufficient to "shove aside" adjacent molecules to cause a local flow event [FIFTH INTERNATIONAL DISCUSSION MEETING ON RELAXATION IN COMPLEX SYSTEMS; Dyre,JC; July 2005)]. In a glass, as well as in a viscous liquid, a local stress is relieved by diffusion, a process described on the molecular level as structural relaxation. Diffusion can occur when there is sufficient local energy to overcome "molecular friction". "Jump diffusion" equations are often better than the Einstein-Stokes equation for determining diffusivity in viscous liquids near Tg. The relief of local stresses by intentional elevation of temperature (to shorten the time for structural relaxation) is called annealing. Natural relief of local stresses due to diffusion over time is called aging.
For supercooled liquids or amorphous (glassy) systems relaxation time describes how rapidly the system reverts to that of a supercooled liquid or glass in equilibrium when subjected to a local stress. Although a supercooled viscous liquid or glass can be described as being "metastable" (or out-of-equilibrium) by not being crystalline, the liquid or glass can also be described as being "relatively out-of-equilibrium" when subjected to a local stress. In this sense, structural relaxation and relaxation time can be applied to glasses and supercooled liquids in the same manner as they would be applied to any viscous liquid above its melting point.
Molecular mobility decreases with increasing viscosity. Or, stated another way, molecular mobility is the reciprocal of viscosity. For glass-forming agents there is a significant increase in viscosity associated with the glass transition temperature (Tg). For cryoprotectants, such as those used in cryonics, hydrogen-bonding is the main constraint upon molecular motion. Cryoprotective substances with higher Tg (generally those with higher molecular weight) have hydrogen bonds that are longer and weaker than those for substances with lower Tg — molecular translational and rotational mobility is demonstrably reduced at Tg [CARBOHYDRATE RESEARCH; Wolkers,WF; 339(6):1077-1085 (2004)].
Pea seeds that can germinate after 3 to 50 years at 20ºC can survive from 250 to 2,466 years at 0ºC — an effect due to the differences in molecular mobility in the vitrified cytoplasm [PROCEEDINGS OF THE NATIONAL ACADEMY OF SCIENCES (USA); Bultink,J; 97(5):2385-2390 (2000)]. If vitrification could reduce molecular mobility to that of a crystalline state, residual heat energy would be restricted to vibrational motion only, which is far less capable of damaging molecular structures (and of devitrification) than rotational and translational motion. Glasses need not flow and, indeed, it is an urban legend that glass has flowed in ancient window panes.

|
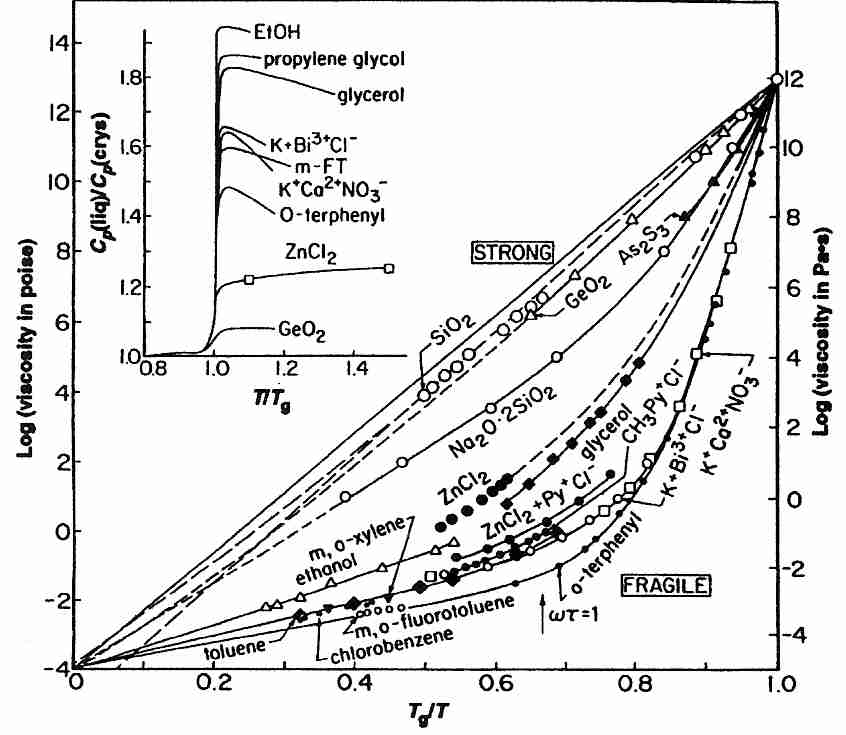
Vitrifying liquids have been classified as "strong" or "fragile". The term fragile is confusing because it does not refer to the tendency to break under mechanical stress, but rather to a highly rapid rise in viscosity as temperature approaches Tg from above. Substances which are called fragile tend to have more ionic bond types (or hydrogen bonds), whereas substances which are strong (and show a modest decline in viscosity above Tg) have more covalent bonding. "Gripping strength" changes more radically for ionic bonding near Tg. Covalent bonds are stronger (less fragile), and groups of molecules held together by covalent bonds are less susceptible to molecular phase changes just above Tg. Glycerol-type cryoprotectants (which cohere mainly by hydrogen bonding) are more "fragile" than vitreous silica (which has covalent coherence), but are less "fragile" than ionic substances.
A mixture of melted anhydrous salts of KNO3 and Ca(NO3)2 in molar proportion 3:2 (KNC — K+Ca+2NO3−) is an extremely fragile liquid (as can be seen in the diagram). In general, very fragile liquids (such as KNC) tend to have high heat capacity change at Tg, but liquids which hydrogen-bond (such as cryoprotectants) have a higher heat capacity change at Tg, but are only moderately fragile (see diagram inset).
On the Kelvin temperature scale it is a rule of thumb that Tg occurs at about two-thirds the value of the melting temperature (Tm). Substances for which Tg/Tm is significantly greater than 2/3 are fragile [THERMOCHIMICA ACTA; Hancock,BC; 380:95-107 (2001)].
The linear character of strong glass-formers seen on a logarithmic plot of viscosity (η) against the reciprocal of temperature (1/T) demonstrates an Arrhenius equation behavior, with viscosity rather than reaction rate (k) as the right-hand term:
k = A exp [−Ea/RT] (Arrhenius Equation)
where k is reaction rate, A is a constant, exp indicates that the term in square brackets is a power of e (2.71828), Ea is the activation energy, R is the universal gas constant and T is temperature. An equation where viscosity (η) takes the place of reaction rate is fitting for strong (rather than fragile) glass-formers, for which molecular mobility decreases exponentially with temperature.
For fragile glass-formers (such as the cryoprotectants used in cryonics) an almost double-exponential relationship exists between viscosity and temperature. For fragile glass-formers the plot of viscosity against reciprocal of temperature above Tg is most often fitted to the empirical Vogel-Fulcher-Tammann equation (VFT):
η = A exp [DTo/(T-To)]
where A is a constant, exp indicates that the term in square brackets is a power of e (2.71828), To is the temperature at which molecular mobility is zero (the VFT temperature, where viscosity becomes infinite when T = To), and D is a constant corresponding to fragility. Increasing values of D change the solution from fragile to strong, so fragility has been defined as the inverse of D. In practice, however, real solutions rarely fit the VFT equation over a full range of values [CHEMICAL REVIEWS; Angell,CA; 102:2627-2650 (2002)]. The most fragile liquids (such as KNC) fit the VFT curve poorly, whereas moderately fragile liquids (such as glycerol) fit the curve very well. The ratio To/Tg has also been used as a scaling parameter for deviation from Arrhenius behavior, for a ratio between 0 (strong) and 1 (fragile) [JOURNAL OF NON-CRYSTALLINE SOLIDS; Hodge,IM; 202:164-172 (1996)].
Shear stress relaxation time (τs) is often calculated from viscosity (η) by the Maxwell equation:
η = G∞τs or τs = η/G∞
where G∞ is the instantaneous ("infinite frequency") or unrelaxed shear modulus as measured on a time scale so short that a liquid does not have time enough to flow in response to an applied stress. G∞ changes with temperature more rapidly for fragile liquids. Relaxation time is the average time it takes for viscous fluid to eliminate all strain associated with an imposed fluid stress. A liquid is "solid-like" on time scales much shorter than τ. A common (but unofficial) definition of Tg is a viscosity of 1012 Pascal-seconds (equivalent to 1013 Poise) or a relaxation time of 100 seconds (a definition that has been largely displaced by calorimetric determination).
The VFT equation is sometimes written directly in terms of relaxation time as:
τs = τo exp [DTo/(T-To)]
with τo assigned a value of 10−14 seconds, which can give a good fit for liquids of intermediate fragility. Because τo and To are constants, the VFT equation is often written using constants A, B, and C in the place of τo, DTo and To, respectively.
In the Arrhenius model, activation energies (Ea) may increase by a factor of three below Tg [PROCEEDINGS OF THE NATIONAL ACADEMY OF SCIENCES (USA); Bultink,J; 97(5):2385-2390 (2000)]. Activation energy changes for the stability of liposomes in sugar glasses have also been reported at Tg [BIOPHYSICAL JOURNAL; Sun,WQ; 70(4):1769-1776 (1996)].
The Kauzmann temperature (TK, "ideal glass
transition temperature") is a hypothetical temperature at which the
configurational entropy of a supercooled liquid is presumed to be
reduced to that of a crystalline state. The value of TK
is determined from a plot of configurational entropy (Sc)
versus temperature for a cooling glass. [Configurational entropy is also
called positional entropy, defined as the number of spatial positions
molecules can occupy in a system. Configurational entropy is distinguished
from thermal
entropy JOURNAL OF CHEMICAL EDUCATION, Lambert,JL;
84(8):1548-1550 (2007)]. Extending the values of the entropy cooling curve to
the point where it intersects the entropy of the crystal gives TK.
Extending the line further gives rise to the "Kauzmann Paradox", an
"entropy catastrophe" at which the supercooled liquid would have
a lower entropy than the
crystal [JOURNAL OF THE INDIAN INSTITUTE OF SCIENCE; Rao,KJ; 81:3-13
(Jan-Feb 2001)].
| Kauzmann Temperature | Kauzmann Paradox |
![[ Kauzmann Temperature ]](./Kauzmann.jpg)
|
![[ Kauzmann Paradox ]](./Paradox.jpg)
|
|---|
In real systems supercooling does not continue indefinitely, and the impossible result associated with the TK "catastophe" is avoided by glass formation. Nonetheless, heat capacity and other variables at temperatures below Tg approach those of a crystal, indicating that the changes in molecular structure associated with Tg reduce translational and rotational motion of molecules to "nearly the immobility" associated with a crystal [JOURNAL OF PHARMACEUTICAL SCIENCES; Zhou,D; 91(8):1863-1872 (2002)].
TK is a hypothetical thermodynamic temperature for which the mobility of molecules is proposed to be equivalent to that in a crystal (close to, but not necessarily, zero). To is a hypothetical kinetic temperature representing infinite viscosity (zero mobility) — determined by empirical fitting of the VFT equation at temperatures above Tg.
|
Cooling at rates so fast that Tg cannot be measured during the cooling process ("hyperquenching") is a useful tool for researchers studying the mechanisms of relaxation and annealing because glasses formed under these conditions have such high relaxation times [JOURNAL OF NON-CRYSTALLINE SOLIDS; Wang,L; 353(41-43):3829-3837 (2007)]. The fictive temperature (Tf) is the temperature at which an equilibrium supercooled liquid has the same configurational entropy (or enthalpy) as the glass. Above Tg (ie, in liquid equilibrium) Tf = T. Tf is highly dependent upon cooling rate. In hyperquenching Tf is determined after the solid has formed. Under these conditions, Tg is determined upon re-heating the glass, and is generally defined as a relaxation time of 100 seconds or a viscosity of 1012 Pascal-seconds [JOURNAL OF CHEMICAL PHYSICS; Yue,Y; 120(17):8053-8059 (2004)]. Tf is bounded by Tg and TK, ie, TK < Tf < Tg [JOURNAL OF PHYSICAL CHEMISTRY; Shamblin,SL; 103:4113-4121 (1999)].
Below Tg relaxation is so slow that relaxation time can be described as a function of time, ie, the relaxation time changes as the relaxation progresses. Tf is a function of time which will approach an imposed temperature T1. Tf can be used to write a modified VFT equation (a form of the Adams-Gibbs equation) for which the time dependence of τs is completely determined by changes in Tf:
τs = τo exp [DTo/(T(1 - (To/Tf))]
[PHARMACEUTICAL RESEARCH; Mao,C; 23(8):1906-1917 (2006)].
|
For strong glass-formers TK can be as much as twice the value of To, but for fragile substances TK is close to the value of To. For ethylene glycol TK is 5% greater than the value of To [PHYSICAL REVIEW LETTERS; Tanaka,H; 90(5):055701; 1-4 (2003)]. For glycerol TK was found to be −138ºC and To was −145ºC. For ethylene glycol TK was −158ºC and To was −164ºC [JOURNAL OF RESEARCH OF THE NATIONAL INSTITUTE OF STANDARDS AND TECHNOLOGY; C.A. Angell; 102(2):171-185 (1997)]. (The values are for pure solutions rather than solutions a concentrations needed to vitrify.) These results are not far from the estimate that for fragile amorphous materials, such as the cryoprotectants used in cryonics, the temperature (To) at which average molecular mobility "approaches zero" is estimated to be about 50ºC below Tg [THERMOCHIMICA ACTA; Hancock,BC; 380:95-107 (2001)]. Tg for vitrification solutions used in cryonics — at the concentrations needed to vitrify — is close to −124ºC. Calculation of TK and empirical determination confirm that measurable molecular mobility exists in amorphous solids below TK [BIOPHYSICAL JOURNAL; Walters,C; 86(2):1253-1258 (2004)]. Relaxation times of 3 to 5 years have been determined at temperatures close to 50ºC below Tg for amorphous sorbitol, sucrose, trehalose, and indomethacin [JOURNAL OF PHYSICAL CHEMISTRY; Shamblin,SL; 103:4113-4121 (1999)]. Dialectric loss in glass insulators hundreds of degrees below Tg has been attributed to mobile alkali ions and protons [JOURNAL OF APPLIED PHYSICS; Section C; Angell,C.A.; 88(6):3113-3156 (2000)].
These estimates would mean that a storage temperature for cryonics patients in the −165ºC to −175ºC range would be required to prevent the effects of molecular mobility, namely devitrification and direct molecular damage. These temperatures are well below proposed Intermediate Temperature Storage (ITS) temperatures intended to prevent cracking.
At temperatures above 20% greater than Tg (often referred to as Tc, critical temperature) translational and rotational diffusion is inversely proportional to viscosity according to the Einstein-Stokes and Debye equations, respectively. Between Tc and Tg the Debye equation for rotational diffusion remains valid, but the Einstein-Stokes equation breaks down. Near Tg molecular translational motion in very fragile glass-forming liquids can be as much as two orders of magnitude faster than would be predicted by Einstein-Stokes based on the viscosity [JOURNAL OF CHEMICAL PHYSICS; Cicerone,MT; 104(18):7210-7218 (1996)]. Glycerol is strong enough that the Einstein-Stokes relation remains valid to the lowest temperatures studied [JOURNAL OF APPLIED PHYSICS; Section A.1.9.1; Angell,C.A.; 88(6):3113-3156 (2000)], and this probably also applies to ethylene glycol, which is of similar fragility/strength.
|
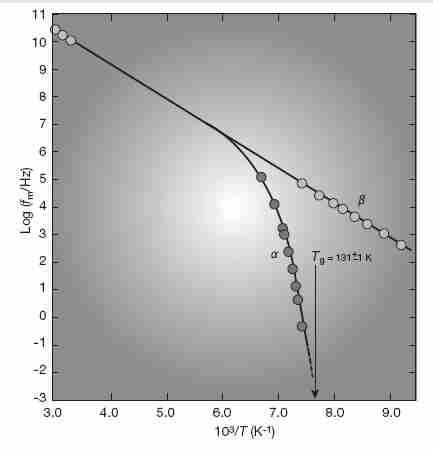
Also in the region moderately above Tg, the single relaxation mechanism diverges increasingly into a slow (α) and fast (β) relaxation mechanism as Tg is approached from above. The slow (α) relaxation process (which characterizes fragile liquids) is associated with the molecular rotation & relaxation of flow in viscous fluids, and displays non-Arrhenius (more than exponential) behavior. By contrast, the fast (β) relaxation process (characteristic of strong liquids) is associated with vibrational excitation (spin-lattice relaxation), and displays Arrhenius behavior [JOURNAL OF NON-CRYSTALLINE SOLIDS; Sokolov,AP; 172/174:138-153 (1994) and THEMOCHEMICA ACTA; Moynihan,CT; 280/281:153-162 (1996)]. The slow (α) relaxation process vanishes below Tg.
Below Tg (about −124ºC for vitrification solutions used
in cryonics) relaxation times
should follow an Arrhenius form, although there is still some deviation for fragile
systems [JOURNAL OF APPLIED
PHYSICS; Section B2; Angell,C.A.; 88(6):3113-3156 (2000)]. As temperature drops
increasingly below Tg, non-Arrhenius behavior rapidly
diminishes [BIOPHYSICAL JOURNAL; Walters,C; 86(2):1253-1258 (2004)]. Most
sub−Tg non-Arrhenius behavior is seen in heterogenous molecular
systems where small ionic species retain molecular mobility within larger
molecular species that become immobilized at Tg [JOURNAL OF
NON-CRYSTALLINE SOLIDS; Mizuno,F; 352(42/49):5147-5155 (2006)]. Fragile systems
are more heterogenous than strong systems. Non-Arrhenius behavior is due to structural
changes, and when structural changes become arrested at Tg
non-Arrhenius behavior disappears below Tg. But even though structure
is fixed, flow can happen in a vitrified solid. Flow even happens in a crystal by
movement of defects. For similar reasons a glass that is well below Tg
will display viscosity (molecular mobility) that is an Arrhenius function of
temperature — possibly all the way down to zero Kelvin.
| Viscosities at Tg | Slopes at Tg | Slopes below Tg |
|---|---|---|
![[ Viscosities at T<sub>g</sub> ]](./Fragile_Viscosity.jpg)
|
![[ Slopes at T<sub>g</sub>]](./TgSlope.jpg)
|
![[ Slopes below T<sub>g</sub> ]](./TwoSlopes.jpg)
|
Insofar as the non-Arrhenius component of the temperature/viscosity relation disappears rapidly below Tg it seems reasonable to extrapolate an Arrhenius (strong) line to below Tg to estimate the viscosity of the vitrified solids (glasses) at sub-Tg temperatures. But the first graph shown in this section (labeled "Strong and Fragile Glass-Formers above Tg") shows all the glass-forming liquids having a viscosity of 1012 Pascal-seconds at Tg. (In the 1980s, when that first graph was made, Tg was typically defined as the temperature where viscosity equals 1012 Pascal-seconds.) As the graph in the first frame above shows, when Tg is determined calorimetrically viscosity at Tg can range from about 108 Pascal-seconds (for the most fragile liquids) to 1012 Pascal-seconds (for the most strong liquids). As shown in the graph in the second frame, slopes for fragile liquids near Tg are in the range of about 50 on a plot of Tg/T against log10 η. As shown in the graph in the third frame, the slope of the line is discontinuous and drops from about 50 to about 10 with the transition to the solid state below Tg. Viscosity in the solid state is different from viscosity in the liquid state, and it has been called "creep viscosity" to indicate flow by movement of defects (which can also happen in a crystal).
The only cryoprotectant shown in the first graph in this section is glycerol, which has a fragility very close to that of ZnCl2. Glycerol is not shown in the graph of the first frame above, but ZnCl2 is shown to have a viscosity at Tg of 1012 Pascal-seconds, which can be taken as a proxy for the viscosity at Tg for the cryoprotectants used in cryonics. A line intersecting log10 η of Tg/T = 1.0 at 12 with a slope of 10 will have a y-intercept of 2. So the Arrhenius line for estimating values of log viscosity above 1.1 Tg/T (i.e., more than 10% below Tg) would be the simple linear equation:
log10 η = 10 (Tg/T) + 2 where η is the viscosity in Pascal-seconds.
I have used this formula to get estimates for values of η at various temperatures using −123ºC (150 K) as the value of Tg (the approximate Tg of vitrification mixtures used in cryonics). Intermediate Storage Temperature (ITS) is of special interest in cryonics because of the belief that storing patients at this temperature there would be much less cracking due to thermal stress, and this temperature would be adequate for cryopreservation of decades, if not centuries.
For Intermediate Storage Temperature −135ºC (about 138 K) Tg/T = (150/138) = 1.087 and the formula gives:
log10 η = (10*1.087) + 2 = 12.9 or η = 1012.9 Pascal-seconds
For the approximate values of TK or To temperature −165ºC (about 108 K) Tg/T = (150/108) = 1.39 and the formula gives:
log10 η = (10*1.39) + 1 = 15.9 or η = 1015.9 Pascal-seconds
For liquid temperature −196ºC (about 77 K) Tg/T = (150/77) = 1.95 and the formula gives:
log10 η = (10*1.95) + 1 = 21.5 or η = 1021.5 Pascal-seconds
Thus, at Intermediate Storage Temperature (−135ºC) ethylene glycol is about 1015 (one quadrillion) times more viscous than it is at 25ºC (0.0161 Pa·s) and at liquid nitrogen temperature is nearly 1024 (one septillion) times more viscous. (Corn syrup is about 85 times more viscous than ethylene glycol is at 25ºC, and ethylene glycol is about 18 times more viscous than water at that temperature).
There are actually two equations in kinetic theory that are called Einstein relations, the aforementioned Einstein-Stokes equation (Stokes-Einstein relation):
kBT
D = ------
6πrη
and the Einstein-Smoluchowski relation:
D = μpkBT
which uses mobility μp as drift velocity resulting from an applied force μp = Vd/F. Eliminating D and solving for μp gives the simpler equation:
1
μp = ------
6πrη
The drift mobility μp will be in units of meters per second per Newton of applied force. (Note that Pa·s = kg/(m·s) and N = (kg·m)/s2) But the only force experienced by a cryonics patient would be the force of gravity, opposed by an equal and opposite force below the patient — which is why the cryonics patient does not move. On the molecular level forces would be random, resulting in a Brownian motion.
Using the Einstein-Stokes equation to find the diffusion coefficient (D) for a given temperature (T) and viscosity (η) provides the means of determining typical displacement of a water molecule (radius = 1.4 x 10−10 meters) after a century of Brownian motion in a cryonics patient. The value of kB (Boltzmann's constant) is 1.38 x 1023 Joules/Kelvin, where J/K = (kg·m2)/(s2K). Thus, the Einstein-Stokes equation yields:
(1.38 kg·m2/s2K)(138K)
D at −135ºC (~138K) = --------------------------------------------------
= 9.09 x 10−26 m2/s
6(3.1416)(1.4 x 10−10 m)(1012.9 kg/(m·s))
Similarly, D at −165ºC (~108K) = 7.11 x 10−26 m2/s and D at −196ºC (~77K) = 1.27 x 10−34 m2/s
The typical distance that a water molecule will be displaced from its initial position after a time t can be estimated by calculation of the variance (σ2) of the Green's function of the diffusion equation in three dimensions (by relating Brownian motion to a random walk):
σ2 = 6 Dt
Using a value of t equal to one century (3.156 x 109 seconds based on 365.2425 days per year) of storage for a cryonics patient, and taking the square root of the variance gives the typical distance (standard deviation) a water molecule will have traveled from its point of origin for the diffusion constant (D) for a given temperature and viscosity.
For Intermediate Storage Temperature (−135ºC , ~138K) the typical distance a water molecule will have been displaced over the course of a century is about 40 nanometers, whereas for −165ºC (~108K) the displacement is about one nanometer and at liquid nitrogen temperature (−196ºC ,~77K) the distance is about one-and-a-half picometers. All of these values would seem acceptable in a cryonics patient if the typical linear distance traveled by the water molecule were the same as the total distance. But the actual total linear distance (path length) traveled by the water molecule due to Brownian motion will be vastly greater than the typical displacement from the point of origin. Doing the same calculation for a water molecule at room temperature (25ºC , about 298K) using the viscosity of ethylene glycol (0.0161 Pa·s) gives a typical distance of about 1.4 meters. A water molecule at room temperature would travel a vastly greater path-length than 1.4 meters over the course of a century.
Also worrisome is the possiblility of ions within the glass that are far more mobile than the molecules constituting the glass. An ionic species (probably protons) in trimethylammonium dihydrogen phosphate glass is nine orders of magnitude more mobile than the glass molecules — and sodium ions in sodium disilicate glass are twelve orders of magnitude more mobile than the glass molecules [JOURNAL OF NON-CRYSTALLINE SOLIDS; Mizurno,F; 352(42/49):5147-5155 (2006)]. Water molecules can be quite mobile when in polydextrose glass, and carbon dioxide is mobile in polyvinyl alcohol (same reference).
But, molecular mobility is not lethal for northern wood frogs that can spend weeks to months in a semi-frozen state [THE FASEB JOURNAL; Costanzo,JP ; 9(5):351-358 (1995)]. The most damaging effects of molecular mobility at temperatures below Tg should be either from water molecules forming crystals or from mobile free radicals. Concerning the latter, cryobiologist Peter Mazur was quoted at the beginning of this piece as saying: "...there is no confirmed case of cell death ascribed to storage at −196ºC for some 2-15 years and none even when cells are exposed to levels of ionizing radiation some 100 times background for up to 5 yr." [AMERICAN JOURNAL OF PHYSIOLOGY; Mazur,P; 247(3 Pt 1):C125-C142 (1984)].
More experiments exposing tissues to ionizing radiation could be helpful in assessing the safety for cryonics patients of various sub−Tg temperatures above liquid nitrogen temperature. Experiments should also be done to determine the possibility of ice formation at cryogenic temperatures over long periods. More information is needed before it can be stated with certainty that damage due to molecular mobility at Intermediate Storage Temperature would not be worse than the effects of cracking damage.
[NOTE: Sharper increases for viscosity with declining temperature were estimated for 7.05 M DMSO (Tg = −132ºC) with viscosity η = 1018 Pascal-seconds) for −140ºC CRYOBIOLOGY; Rabin,Y; Figure 11; 53(1):75-95 (2006), but JOURNAL OF APPLIED PHYSICS; Section A.1.2.1; Angell,C.A.; 88(6):3113-3156 (2000) and other citations given above make it clear that this figure is exaggerated because it is based upon an inappropriate application of the VFT equation below Tg].